强化学习——多臂老虎机问题
作者:oneraynyday
编译:Bot
编者按:无论有没有去过赌场,相信大多数人都不会对老虎机感到陌生。作为赌场里最常见的娱乐设备,老虎机不仅在现实中广受人们欢迎,它也频繁出现在电视电影乃至动画片中,连一些常见的APP里都有它的身影。

往机器里投入硬币后,玩家需要拉下拉把转动玻璃框中的图案,如果三个图案一致,玩家能获得所有累积奖金;如果不一致,投入的硬币就会被吞入累积奖金池。这个问题看似简单,但很多人也许都忽视了,其实它和围棋、游戏一样,也是个强化学习问题。
首先,我们要明确一点——老虎机问题是表格型解决方案工具的一种。之所以这么说,是因为我们可以把所有可能的状态放进一个表格中,然后让表格告诉我们需要了解的问题状态,继而为解决问题找出切实的解决方案。
假设我们有一台K臂老虎机,每根拉杆都能提供固定的一定数额的金钱,一次只能拉下一根拉杆,但我们不知道它们的具体回报是多少。在这个情景中,k根拉杆可以被视为k种不同的动作(action),拉下拉杆的总次数T是我们的总timestep。整个任务的目标是实现收益的最大化。
设在第 




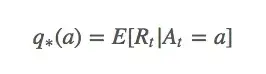
这个等式表示的是无论何时,如果我们选择动作 

把上面这个句子再读三四遍,你觉得它行得通吗?如果我们事先已经知道拉下这个拉杆的最大收益是多少,那出于贪婪的目的,我们肯定每次都会选最好的动作,然后使最终回报最大化。但在强化学习问题中,贪婪算法并不一定等同于最优策略,这一步的贪婪可能会对下一步产生负面影响。
虽然很困难,但我们真的很想实现 



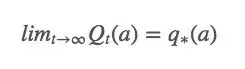
那么我们又该怎么获得 
注:上文中的回报(reward)和动作值(value)不是同一个概念。回报指的是执行动作后的当场回报,动作值是一个长期的回报。如果你吸毒了,一小时内你很high,回报很高,但长期来看,你获得的动作值就很可怕了。需要注意的是,因为老虎机只需要一个动作,所以这里的 

函数
表示从状态
出发,执行动作
后再使用策略
带来的累计奖赏,称为“状态-动作值函数”(state-action value function)。——周志华《机器学习》
首先,我们需要估计动作值,再据此决定要采取的行动。
估算动作值
求解 
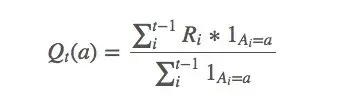
上述等式看起来好像有什么说法,但它其实很简单——选择动作 

换句话说,它意味着 

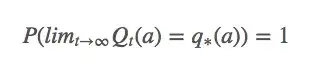
比起概率收敛,这种收敛更强大,但它其实也没法保证 
动作选择规则:贪婪
“贪婪者总是一贫如洗。”当面对巨大诱惑时,一些人会因为贪婪越过自己的底线,去吸毒,去犯罪,但他们在获得短暂快感的同时也失去了更多东西。强化学习中同样存在类似的问题,如果它是贪婪的,它会找出迄今为止最大的动作值:
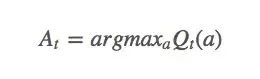
并依据这个动作值去选择每一步动作。这样做的后果是智能体从头到尾只会选择同一套动作,而从不去尝试其他动作,在很多情况下,这样的策略并不是最优策略。
动作选择规则:ϵ-Greedy
那么我们该怎么纠正它的贪婪?之前我们在《强化学习——蒙特卡洛方法介绍》一文中已经介绍过 




虽然当智能体“头脑发热”时,它还是会义无反顾地贪婪,但相比贪婪策略, 

导致这种现象的主要原因是动作值会随时间推移发生变化,即之前我们研究的是静态的拉杆,而不是随机的、动态的拉杆。以动作值为例,比起我们之前假设的 

依据之前的动作值估计,我们有:
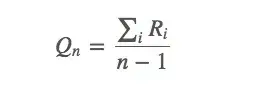
它也可以被写成:
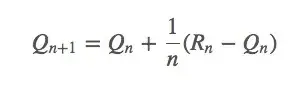
看起来SGD可以在这里发挥一些作用。如果它是平稳的,那 

这里我们把权重 
![α(α∈(0,1])](https://hejiyule.org/wp-content/uploads/2023/07/OvQef4VSx.jpg)
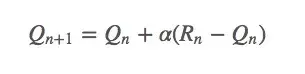
这是一个指数平均值,它在几何上衰减之前回报的权重。设函数 




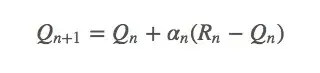
为了保证上式能收敛,我们还需要一些其他条件。
条件一
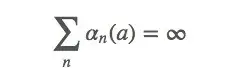
上式表示对于任何初始值 

条件二
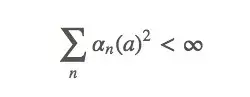
这个式子表示这些timestep将“足够小以确保能收敛到一个小值”。简而言之,第二个条件保证最终timestep会变小,以保证收敛。
既然如此,我们之前为什么要设 ![α_n(a)=α∈(0,1]](https://hejiyule.org/wp-content/uploads/2023/07/654G5pZ.jpg%3D%CE%B1%E2%88%88%280%2C1%5D)
这些猜想都是正确的,但 ![(0,1]](https://hejiyule.org/wp-content/uploads/2023/07/ZUqlUGlTdG.jpg)




最佳动作值时非平稳的,我们不想收敛到一个特定的价值。和记娱乐下载
到目前为止,我们必须随机设定 


这样之后,因为 

这种方法是可行的,在某种程度上,如果时间充裕,这个过程也可以被看作是模拟退火。但从整体来看,乐观初始值前期的大量“exploration”是不必要的,它对于非平稳问题来说不是最好的答案。
在机器学习系统中,Bias与Variance往往不可兼得:如果要降低模型的Bias,就一定程度上会提高模型的Variance;如果要降低Variance,Bias就会不可避免地提高。针对两者间的trade-off,下面的式子是一个很好的总结:
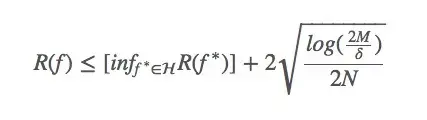
其中,
是假设
的(理论上)的风险;
是在假设集
中,假设
的最小风险;
是假设集
的大小;
是其中的样本数;
是一个常数(如果非要知道这个常数是什么,只能说它是我们选择一个差的假设的概率)。
这里有两个重点:
- 样本数量非常少,我们的边界非常松散。我们不知道目前的假设是否是最好的假设。
- 我们的假设越大,PAC(近似正确)学习的约束就越松散。
置信上限(UCB)是一个非常强大的算法,它可以用类似Bias-Variance权衡的方法来解决不同的问题。在老虎机问题中,我们可以把timestep 

也会逐渐增加,相应的

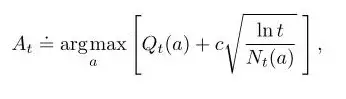
每选一次 
增加;另一方面,每一次选择了


不会改变,不确定评估值会增加。
截至目前,我们一直在努力估计 
设动作偏好为 ,它和回报无关,只是一个动作相对于另一个动作的重要性。那么

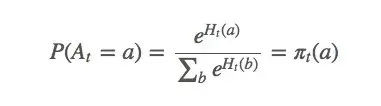
对于这个式子,我们该怎么基于梯度计算最大似然估计?首先,我们对 做梯度上升,因为它是我们的变量。我们想最大化

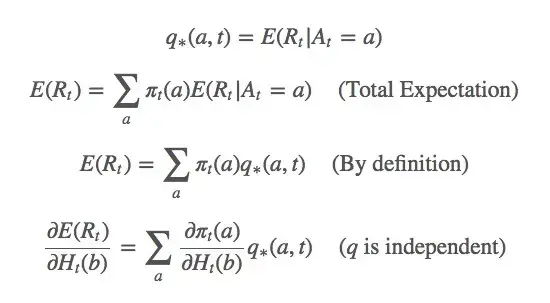
的更新规则如下所示:
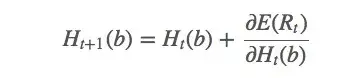
gibbs分布分解:
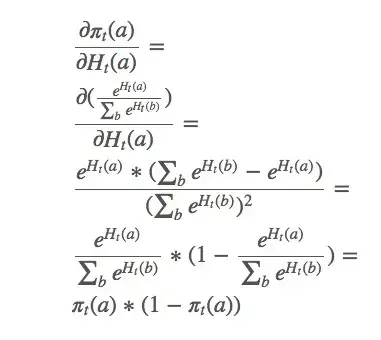
这只是整个梯度的一个偏导数。那么 
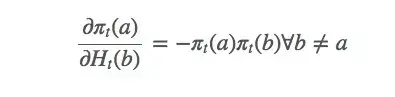
由此可得:

因为:
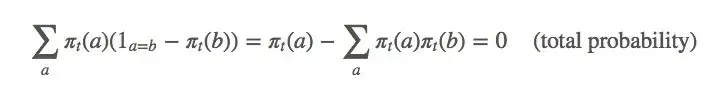
相应的,这个等式也是成立的:
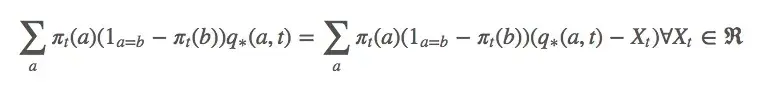
由上述等式可得:
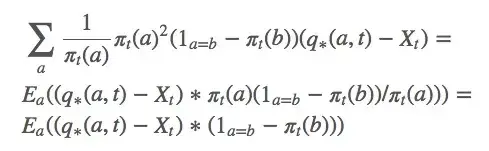
因为 




计算梯度后获得新的更新规则:
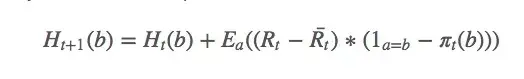
其中 



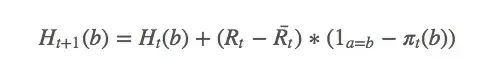
选择动作的简单方法是计算 ,问题就解决了。
下面是上述算法的一个比较图:
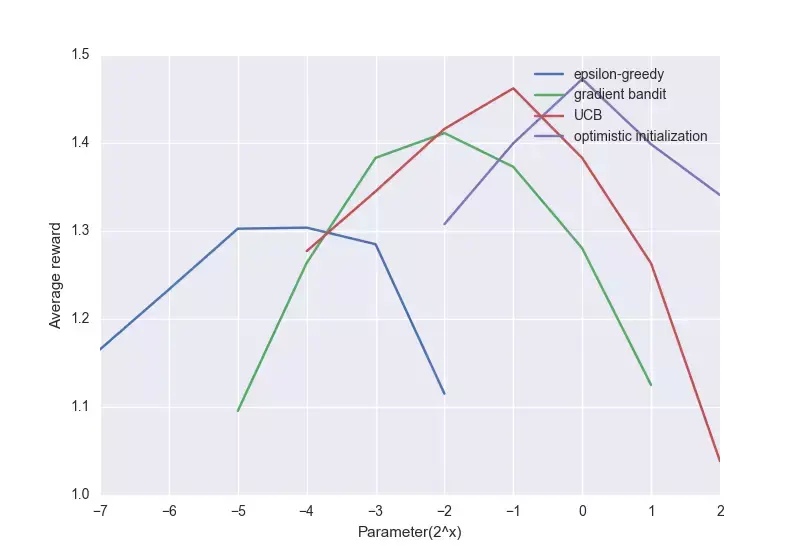
88老虎机
尽管简单的方法表现不太好,但对很多强化学习问题来说,它们也称得上是最先进的算法了。


 表示从状态
表示从状态  出发,执行动作
出发,执行动作  带来的累计奖赏,称为“状态-动作值函数”(state-action value function)。——周志华《机器学习》
带来的累计奖赏,称为“状态-动作值函数”(state-action value function)。——周志华《机器学习》 是假设
是假设  的(理论上)的风险;
的(理论上)的风险; 是在假设集
是在假设集  中,假设
中,假设  的大小;
的大小; 是其中的样本数;
是其中的样本数; 是一个常数(如果非要知道这个常数是什么,只能说它是我们选择一个差的假设的概率)。
是一个常数(如果非要知道这个常数是什么,只能说它是我们选择一个差的假设的概率)。