求通俗解释下bandit老虎机到底是个什么东西？

单臂one-armed 和多臂multi-armed 的

multi-armed bandit是一个非常经典的模型，当然，该模型有很多变种。我能查到的中文资料基本上都是浓浓的看不懂的翻译腔，用最最通俗的语言描述其中最基本的模型应该是这样的

假设你面前有这些色彩斑斓的按钮，按完每个按钮可能有两种情况：从机器里掉出一块钱，或者什么也没有发生

每个按钮出钱的概率是不一样的，也许那个红色的按钮有80%的概率会出钱，而那个右下角灰色的出钱概率为0，按到死都出不了一分钱，当然，在此之前，你对每个按钮出钱的概率的先验知识为0,也就是说你不知道每个按钮出钱的概率是多少。

而我们的目标是，在有限次的按按钮过程中(比如按1000次)，获取的钱越多越好，应该以怎样的策略呢？

这个问题的麻烦之处在于，寻找最优的按钮和获得最大值之间的平衡!

举个例子

假设你开启上帝模式，知道这些按钮里概率最高的是红色按钮，有80%的概率出硬币，那最好的策略显然就是死命的对那个红色按钮怼，那么1000次尝试你会得到钱数的期望是800块，并且没有比这更好的策略了。

但在不知道这些知识的前提下，我们怎么做？小蠢是这样做的，每个按钮按三次，然后看出钱的多少，然后以后的每次都对着三次出钱最多的那个怼，但出钱概率70%的按钮也可能按三次一次都没出钱，出钱概率10%的按钮也可能连续按三次都出钱了，这样做显然不科学！

那增加实验次数行不行？我们每个按钮按50次，那么可以假设它收敛到期望了，但如果我们有20个按钮呢？1000次机会全给你做实验了，即使50次实验能得到所有按钮的准确的出钱概率，你也用光了1000次机会，然后把这些机会全部平均分给所有按钮，和你随机乱按没有区别。（摔桌，宝宝不玩了）

当然你也可以提出各种不同的策略、算法，但是归根结底，这个问题的本质就是寻找最优的按钮和获得最大值之间的平衡!

然后毕竟它只是个模型，传染病模型都可以用到和它根本不搭界的消息传播模型上，它能使用到的领域基本上就是这种寻找最优-获得最大值矛盾的地方，举个例子，临床试验：我们既要保证得出的每种药品治愈患者的概率较为准确，又要使得最后参加试验的患者治愈率最高；广告投放：我们在找到最能吸引点击率的广告的过程中又要使得，过程中广告的点击率尽可能最大。

有很多奇奇怪怪的策略来解决这个问题，比如其它楼链接中UCB族算法，当然还有用的比较多，可能性能更好的[1] Thompson sampling。

以上

reference：

[1] O. Chapelle and L. Li. An empirical evaluation of thompson sampling. In NIPS, 2011.

关于这个问题，我们想采用微软亚洲研究院资深研究员陈卫在中国理论计算机年会上的报告“在线组合学习”进行回答，解读多臂老虎机和组合在线学习之间的关系。

————这里是正式回答的分割线————

赌场的老虎机有一个绰号叫单臂强盗（single-armed bandit），因为它即使只有一只胳膊，也会把你的钱拿走。而多臂老虎机（或多臂强盗）就从这个绰号引申而来。假设你进入一个赌场，面对一排老虎机（所以有多个臂），由于不同老虎机的期望收益和期望损失不同，你采取什么老虎机选择策略来保证你的总收益最高呢？这就是经典的多臂老虎机问题。

这个经典问题集中体现了在线学习及更宽泛的强化学习中一个核心的权衡问题：我们是应该探索（exploration）去尝试新的可能性，还是应该守成（exploitation），坚持目前已知的最好选择?在多臂老虎机问题中，探索意味着去玩还没玩过的老虎机，但这有可能使你花太多时间和金钱在收益不好的机器上；而守成意味着只玩目前为止给你收益最好的机器，但这又可能使你失去找到更好机器的机会。而类似抉择在日常生活中随处可见：去一个餐厅，你是不是也纠结于是点熟悉的菜品，还是点个新菜？去一个地方，是走熟知的老路还是选一条新路？而探索和守成的权衡就是在线学习的核心。

多臂老虎机的提出和研究最早可以追述到上世纪三十年代，其研究模型和方法已有很多。其中一类重要的模型是随机多臂老虎机，即环境给予的反馈遵从某种随机但未知的分布，在线学习的过程就是要学出这个未知分布中的某些参数，而且要保证整个学习过程的整体收益尽量高。这其中最有名的一个方法是UCB（Upper Confidence Bound）方法，能够通过严格的理论论证说明UCB可达到接近理论最优的整体收益。

介绍了多臂老虎机问题，那组合在线学习和它之间有何关联呢？我们继续来看一下组合多臂老虎机（CMAB）问题。在组合多臂老虎机问题中，你一次拉动的不是一个臂，而是多个臂组成的集合，我们称之为超臂（super arm），原来的每个臂我们称之为基准臂（base arm），以示区别。拉完这个超臂后，超臂所包含的每个基准臂会给你一个反馈，而这个超臂整体也给你带来某种复合的收益。

那么如何解决组合多臂老虎机的问题呢？你可能首先想到的就是把每一个超臂看成是经典多臂老虎机问题中的一个臂。但是超臂是多个基准臂的组合，而这样组合的数目会大大超过问题本身的规模——组合问题中经典的组合爆炸现象，因此传统的方法并不适用。所以在线学习不能在超臂这个层次进行，而需要在基准臂层次上进行，并需要与离线组合优化巧妙地结合。我们在ICML2013的论文[2]中给出了组合多臂老虎机的一般框架和基于UCB方法的CUCB算法。CUCB算法将组合优化和在线学习无缝对接实现了前面图示中的反馈回路。较之前的涉及组合多臂老虎机的研究，我们的模型适用范围更广，尤其是我们通过给出收益函数的两个一般条件，能够涵盖非线性的收益函数，这是第一个能解决非线性多臂老虎机问题的方案。我们的工作，包括之后我们和他人的后续工作，都强调对在线学习部分和离线优化部分的模块化处理和无缝对接。也即我们将离线优化部分作为一个黑盒子神谕（oracle），这部分可以由具有相关领域知识的专家来完成。而一旦离线优化问题可以精确解决或近似解决，我们就可以把这个离线算法当作黑盒子拿过来和我们在线学习方法相结合，达到有严格理论保证的组合在线学习效果。这使得我们的方法可以适用于一大批已经有离线优化算法的组合在线学习问题，比如最短路径、最小生成树、最大匹配、最大覆盖等问题的在线学习版本，而不需要对每个问题单独再设计在线学习算法。

在论文“Combinatorial Multi-Armed Bandit: GeneralFramework, Results and Applications”中,我们进一步将组合多臂老虎机模型扩展为允许有随机被触发臂的模型。这一模型可以被用于在线序列推荐、社交网络病毒式营销等场景中，因为在这些场景中前面动作的反馈可能会触发更多的反馈。然而在其理论结果中，我们包含了一个和触发概率有关的项，而这个项在序列推荐和病毒营销场景中都会过大，造成在线学习效果不好。在今年刚被录取的NIPS论文“ Improving Regret Bounds for Combinatorial Semi-Bandits with Probabilistically Triggered Arms and Its Applications”中，我们彻底解决了这个问题：一方面我们论证了序列推荐和病毒营销等满足某种特定条件的问题都不会有这个不好的项，另一方面我们指出在更一般的组合多臂老虎机中这个项又是不可避免的。这是目前研究可触发臂的组合多臂老虎机中最好的一般结果。

除此之外，我们还在与组合多臂老虎机相关的方面做了若干工作，比如如何在反馈受限情况下达到好的学习效果；如何解决先探索再找到最佳方案的组合探索问题；当离线优化基于贪心算法时，如果更好地将离线贪心算法和在线学习相结合；如何在有上下文的场景中解决组合序列推荐问题；以及当超臂的期望收益取决于每个基准臂的随机分布而不仅是每个基准臂的分布均值时，如何同样有效地进行组合在线学习。

————这里是回答结束的分割线————

以上回答摘选自微软研究院AI头条，组合在线学习：实时反馈玩转组合优化。

感谢大家的阅读。

本账号为微软亚洲研究院的官方知乎账号。本账号立足于计算机领域，特别是人工智能相关的前沿研究，旨在为人工智能的相关研究提供范例，从专业的角度促进公众对人工智能的理解，并为研究人员提供讨论和参与的开放平台，从而共建计算机领域的未来。

微软亚洲研究院的每一位专家都是我们的智囊团，你在这个账号可以阅读到来自计算机科学领域各个不同方向的专家们的见解。请大家不要吝惜手里的“邀请”，让我们在分享中共同进步。

也欢迎大家关注我们的微博和微信 (ID:MSRAsia) 账号，了解更多我们的研究。

这篇回答节选自本人在知乎专栏上正在持续更新的一个系列文章的引子：

覃含章：在线学习(MAB)与强化学习(RL)[1]：引言

要了解MAB（multi-arm bandit），首先我们要知道它是强化学习(reinforcement learning)框架下的一个特例。至于什么是强化学习：

我们知道，现在市面上各种“学习”到处都是。比如现在大家都特别熟悉机器学习（machine learning）,或者许多年以前其实统计学习（statistical learning）可能是更容易听到的一个词。那么强化学习的“学习”跟其它这些“学习”有什么区别呢？这里自然没有什么标准答案，我给这样一个解释（也可见Sutton & Barto第二章引言）：在传统的机器学习中，主流的学习方法都是所谓的“有监督学习”（supervised learning），不管是模式识别，神经网络训练等等，你的分类器并不会去主动评价（evaluate）你通过获得的每个样本（sample）所进行的训练结果（反馈），也不存在主动选择动作（action）的选项（比如，可以选择在采集了一些样本之后去采集哪些特定的样本）。意思就是，在这些传统的机器学习方法中（实际上也包括其它无监督学习或者半监督学习的很多方法），你并不会动态的去根据收集到的已有的样本去调整你的训练模型，你的训练模型只是单纯被动地获得样本并被教育(instruct，作为对比，active learning主要就是来解决这一问题的）。

而强化学习主要针对的是在一个可能不断演化的环境中，训练一个能主动选择自己的动作，并根据动作所返回的不同类型的反馈（feedback），动态调整自己接下来的动作，以达到在一个比较长期的时间段内平均获得的反馈质量。因此，在这个问题中，如何evaluate每次获得的反馈，并进行调整，就是RL的核心问题。

这么讲可能还比较抽象，但如果大家熟悉下围棋的AlphaGo，它的训练过程便是如此。我们认为每一局棋是一个episode。整个的训练周期就是很多很多个epsiode。那么每个episode又由很多步（step）构成。

动作——指的就是阿法狗每步下棋的位置（根据对手的落子而定）

反馈——每一次epsiode结束，胜负子的数目。

显然，我们希望能找到一个RL算法，使得我们的阿法狗能够在比较短的epsisode数目中通过调整落子的策略，就达到一个平均比较好的反馈。当然，对这个问题来说，我们的动作空间（action space，即可以选择的动作）和状态空间（state space，即棋盘的落子状态）的可能性都是极其大的。因此，AlphaGo的RL算法也是非常复杂的（相比于MAB的算法来说）。

至于什么是MAB/老虎机问题：

我们先考虑最基本的MAB问题。如上图所示，你进了一家赌场，假设面前有台老虎机（arms）。我们知道，老虎机本质上就是个运气游戏，我们假设每台老虎机都有一定概率吐出一块钱，或者不吐钱（概率）。假设你手上只有枚代币（tokens），而每摇一次老虎机都需要花费一枚代币，也就是说你一共只能摇次，那么如何做才能使得期望回报（expected reward）最大呢？

这就是最经典的MAB场景。那么问题的核心是什么呢？自然，我们应该要假设们是不太一样的（不然怎么摇都一样了），即有一些老虎机比较“好”（更容易吐钱），有一些则比较“差”（不太容易吐钱）。回到RL的框架，我们的动作是什么？即每次摇哪台老虎机。我们的反馈呢？即我们摇了某台特定的老虎机当回合可以观察它吐了钱没有。

这里当然还有个重要的统计学/哲学问题：即我们是贝叶斯人（Bayesian）还是频率学家（frequentist）。对贝叶斯人来说，我们在一进入赌场就对每台老虎机扔钱的概率就有一个先验分布（prior distribution）的假设了，比如一个很常见的我们可以用Beta分布。如果我们认为大概率都应该是0.5，即对半开，而不太可能出现一些很极端的情况，我们就可以选择Beta(1,1)分布作为我们的先验分布。然后在我们真正摇了老虎机之后，根据相应的反馈，我们就可以调整 们相应的后验分布（posterior distribution）。比如如果某台机器摇了四五次一直吐不出钱，我们就应该将这台机器的吐钱概率的分布往左推，因为它的大概率应该是小于0.5的。那么，你的任务便是要在有限的时间内找出 后验分布比较靠右的那些机器（因为他们更容易吐钱），并且尽可能多的去摇这些比较赚钱的机器。

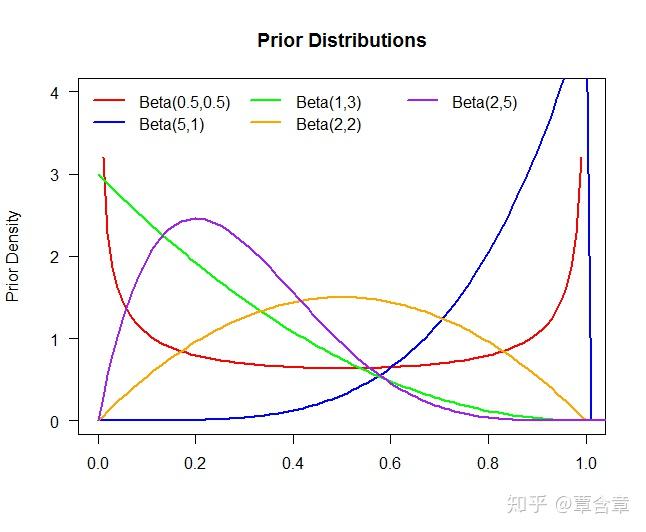
而如果你是频率学家，就没什么先验或者后验分布了，你假设你一开始对这些机器的吐钱概率一无所知。你认为每个机器的 是个确定的值。那么，你的任务就是要在有限的时间内找到那些高 的机器，并尽可能多的去摇它们，以获得更多的回报。那么这里我们注意到这类问题的一大特点，即我们只有次摇机器的机会，如何去平衡这次中exploration（探索）和exploitation（挖掘）的次数。探索意味着广度，比如如果你是频率学家，你一开始什么都不知道，你至少每个机器都需要稍微摇几次（假设，不然问题就无法搞定了）才能对每个机器吐钱概率有个大概感觉。然后，你可能会缩小你的搜索范围，再几台机器里重点实验，最后可能就专门摇一台你觉得最容易吐钱的机器了。当然，我们之后会看到这种办法也未必是最好的。不过这个回答里我们不谈具体的算法，因此这个问题先抛给大家思考了。

本节最后，我们指出这个MAB问题可能的一些（更复杂的）变种。首当其冲的在于，我们前面的讨论默认了环境是不会变化的。而一些MAB问题，这个假设可能不成立，这就好比如果一位玩家发现某个机器的很高，一直摇之后赌场可能人为降低这台机器吐钱的概率。在这种情况下，MAB问题的环境就是随着时间/玩家的行为会发生变化。这类问题，在合理的假设下，也是有不少研究和相应的算法的。目前做的最多的假设，也就是所谓的adversarial bandit（就不是stochastic bandit了），就是说这些会被一个“对手”（也可以看成上帝）设定好。如果这是事先设定好，并且在玩家开始有动作之后也无法更改，我们叫做oblivious adversary setting; 如果这个对手在玩家有动作之后还能随时更改自己的设定，那就叫做adaptive adversary setting, 一般要做成zero-sum game了。此外，最近也有一些随机但nonstationary的假设下的工作。

另外MAB有一类很重要的变种，叫做contextual MAB(cMAB)。几乎所有在线广告推送（dynamic ad display）都可以看成是cMAB问题。在这类问题中，每个arm的回报会和当前时段出现的顾客的特征（也就是这里说的context）有关。同样，今天我们不展开讲cMAB，这会在之后花文章专门讨论。

另外，如果每台老虎机每天摇的次数有上限，那我们就得到了一个Bandit with Knapsack问题，这类问题以传统组合优化里的背包问题命名，它的研究也和最近不少研究在线背包问题的文章有关，之后我们也会专门讨论。还有很多变种，如Lipshitz bandit, 我们不再有有限台机器，而有无限台（它们的reward function满足利普西茨连续性）等等。。题主既然要最通俗的版本，所以这里就不赘述了，有兴趣深入了解的同学们可以考虑关注我的专栏系列文章，主要是让大家有更好的准备去读一些专门的书籍文献~

我从优化角度来说 bandit ，bandit 数学讲严格太多概率计算，十分不直观，所以用不太严谨的方式说。

问题定义：假设收益期望 $Q(a)=\mathbf{E} [r|a]$ 的最优值点为，一开始，我们不知道 Q 的具体数学表达式，Q 也不可导。我们只知道每次输入 $a\in[1,K]$ ，系统黑盒就会按照某个未知分布 P(r|a) 返回 r，如何找到呢？

举个 toy 点的例子，我们不妨给 a 空间分成三个桶，最笨的搜索策略就是暴力遍历各种 a，收集观测值，这样，每个 a 桶内都会累积一定的样本，比如：

$a_1=[r_1, r_2, r_3] \\ a_2=[r_4, r_5] \\ a_3=[r_6, r_7, r_8, r_9]$

剩下的就是用利用这些样本，依靠函数近似拟合出 Q(a)，比如平均法： $\bar{Q}(a_1) = \frac{1}{3}(r_1 + r_2 + r_3) \\$

或者更加复杂的非线性回归方案：

$\lim_{T \to \infty}\min_{\theta} \frac{1}{T}\sum_{t=1}^{T} |Q_{\theta}(a) - r_t(a)|^2 + \theta^2 \\$

然后依靠泛化，取 $\mathbf{argmax}_{a} Q(a)$ 作为的近似解。

换到互联网的说法，就是上线一个流氓策略，调戏用户无限轮，拿到足够的标签，然后跑一个有监督回归任务，只要系统兜底不被击穿，暴力监督方案是一个非常落地其符合国情的算法。

显然，暴力遍历会在前期产生严重亏损，数学上，我们会用利用悔恨度量这种亏损： $R=\sum_{t=1}^T Q(a^*) - \sum_{t=1}^T r_t(a_t)\\$

也就是说，我们搜索最优点，从一无所知到有最终找到，相比一开始就知道最优解是，累积效益能够差多少的问题。这样也很容易理解，前期为了探索，瞎找是不可避免的，悔恨必然是一个随着 T 增大而增大的函数，所以我们不指望找到一个策略让悔恨变成零，而是希望找到某种策略，别让悔恨增长的过快。

下面用非常不严谨的数学，说下悔恨的渐进性质，以及策略迭代的方式。首先，每次迭代一轮策略，我们都可以计算每个 a 下的平均悔恨，比如迭代到第 9 步，有：

$R(a_1)=Q(a^*) - \frac{1}{3}(r_1 + r_2 + r_3) \\ R(a_2)=Q(a^*) - \frac{1}{2}(r_4 + r_5) \\ R(a_3)=Q(a^*) - \frac{1}{4}(r_6 + r_7 + r_8 + r_9)$

总的悔恨为，按照大数定律，我们知道 N 个有限样本做平均得到 $\bar{Q}(a)$ ，和真实期望 Q(a) 之间存在一个 gap，这个 gap 由

$|\bar{Q}(a) - Q(a)| \leq \frac{\epsilon}{\sqrt{N}} \\$

衡量，根据这个 bound，每个 a 对应的悔恨有这么一个不等式：

$R(a_1) < Q(a^*) - Q(a_1) + \frac{\epsilon}{\sqrt{3}}\\ R(a_2) < Q(a^*) - Q(a_2) + \frac{\epsilon}{\sqrt{2}} \\ R(a_3) < Q(a^*) - Q(a_3) + \frac{\epsilon}{\sqrt{4}} \$

一般来说，T 步下的悔恨都有这么一个通用 bound，N_a 是 a 下的累计样本数：

$R<\sum_{a} N_a\times(Q(a^*) - Q(a) + \frac{\epsilon}{\sqrt{N_a}}) \\$

所以，要找到策略让悔恨尽量小，等效于不断调整，也就是调解桶间样本的配比，让 R 的上界增长不要太快。

举个例子，如果配比是 1:1:1，一般只有随机策略才产生这种配比，那么悔恨上界几乎正比于 T，十分不好。

显然，新来一个样本，T+1 步的合理策略，就是找悔恨最小的那个桶，然后将其放入，实际就是选择 $Q(a^*) - Q(a) + \frac{\epsilon}{\sqrt{N_a}}$ 比较小的桶，就给它多增加一个样本，相当于在高置信度下作如下优化选择

$\max_a Q(a) - \frac{\epsilon}{\sqrt{N_a}} < \max_a\bar{Q}(a) + \alpha \frac{\epsilon}{\sqrt{N_a}} \\$

不等式的右边，是要将 Q(a) 这种未知量，依靠高置信度因子 $\alpha$ ，变成能够计算的量，这就是 Upper Confidence Bound (UCB) 的由来。数学上可以证明，UCB 方式下，悔恨增长方式正比于 $\ln T$ 。至于 $\epsilon$ 如何选择，这个需要一点细致计算。

这种情况下，每个桶当中不仅累计了收益，还累积用户特征：

$a_1=[x_1, x_2, x_3] \\ a_2=[x_4, x_5] \\ a_3=[x_6, x_7, x_8, x_9]$

每个桶里，每个用户反馈分别为：

$a_1=[r_1, r_2, r_3] \\ a_2=[r_4, r_5] \\ a_3=[r_6, r_7, r_8, r_9]$

真实收益函数变成，如果我们来了一个新用户 $x_{10}$ ，单纯按照线性 contextual bandit 的算法结果来看，新来样本 $x_{10}$ 的预估收益是加权平均，不再是等权平均。比如，我们预判新用户落到桶会带来收益 $q(x_{10}, a_1)$ ，简单来说是一个相似度和其它用户收益的加权和：

$q(x_{10}, a_1) = r_1S(x_1, x_{10}) + r_2S(x_2, x_{10}) + r_3S(x_3, x_{10}) \\$

如果利用 UCB 去调桶内用户样本配比，新用户将会按照如下方式进入桶内：

$\mathbf{argmax}_{a} q(x, a) + \frac{\epsilon(x)}{\sqrt{N_a}} \\$

说的通俗点，就是先查相似用户，然后再根据其它用户的反馈，估算新来用户的收益，然后加上点不确定度，合并以后最大化，然后把用户塞进去。有趣的是，单纯用户相似性加权这一点，在各种推荐里面都出现，不论数学出发点，还有论证有多绕，总是奇迹般存在这个影子。

理论上，contextual bandit 里面的悔恨非常依赖 S 函数，对于线性的 bandit，S 函数就是某种点乘相似度，不论 S 设计有多复杂，悔恨上界总会被拆分成两部分：

$R<T|Q(x, a^*)- q(x, a^*)| + \sum_{a} N_a\times(q(x, a^*) - Q(x, a) + \frac{\epsilon(x)}{\sqrt{N_a}}) \\$

第一部分的偏差，是我们建模的预估模型 q 没法拟合真实的 reward Q，模型容量低造成的，第二部分就是标准 UCB 带来的 bound，论文一般只计算后者，前者被假设没了。

从上面不太严谨的 bound 也可以看出来，真的做应用的时候，模型拟合不动真实收益函数，前期损失堪比随机策略。所以 Lin-UCB 乃至 sup-Lin-UCB 这些算法，都默认线性能够拟合收益。也导致实际使用当中，收益函数不能够做的太复杂，比如所有兜底惩罚不能够写进收益，就是担心过于复杂的决策边界，会让模型拟合不动，这是很繁琐的 reward engineering 的问题。

如果想提高拟合能力，我们需要复杂一点模型，比如 kernel -UCB，思路也比较简单，就是给特征套一个核函数 $x \to \phi(x)$ ，唯一麻烦的就是求解迭代略复杂。

当然，后面还有如何通过打点日记进行 bandit 的训练，也叫 logged bandit，由于有海量数据做保证，所以深度学习用在 bandit 里头也是有可能的。不过，后者的数学合理性，我目前存疑，故此不展开细说。

在说bandit之前先考虑一个实际问题：假设你来到一个新的城市，你刚开始选择去哪吃饭可能随机选一选，你大概会知道哪些店比较符合你的口味。当你有了一些基本的判断之后，你是会选择吃原来觉得好吃的店呢？还是探索你从来都没有去过的店呢？从来都没有去过的店你可能会觉得更好吃，也有可能不会。人的选择一般都是探索一点点，大部分时候都会选择以前觉得还可以的店。这中间就有个度的问题。在计算机中怎么量化这个度呢，其实还是蛮难的。

可以看出上述问题明显是一个决策性问题，并且是单步决策问题，在强化学习中当前所采取的动作会影响之后的决策，甚至有时候为了获取未来期望的最大回报，我们当前决策可能并不会采取能够获得及时奖励最大的那个动作，像下围棋这种是连续决策问题。单步决策就只有一个状态，选择某个动作，然后游戏结束，开始新一轮游戏。因此Multi-armed Bandit相关的算法的关键都在于如何平衡探索和利用(trade off exploration and exploitation)。这类问题的建模过程可以被用于其它领域，比如像逛淘宝，买东西等等都可以建模成此类问题。甚至可以用于药物研发：

在药物设计问题上面，开发一款药，不同的成分比例对病人的实际应用效果不一样，那究竟是什么样的比例能够把病人快速治好呢？此时动作就变成了选择某个成分的药品，奖励来自病人的反馈(是否痊愈，以及痊愈程度)，我们要做的事情就是用最少的病人，发现这个药物的成分的最佳比例。

bandit老虎机描述的就是这样一类问题的数学模型。(下文对其基本算法展开说明)：

让我们考虑一个最基本的Stochastic Bandits问题，定义如下：

状态集合为single state： $S=\{s\}$ ；一个动作集合，动作此时对应arms，采取某个动作(或者选中某个arm)时，将会得到一个及时奖励的反馈，通常是属于的一个标量。

与传统的强化学习不一样的地方在于这里没有转移函数(transition function)，因为其只有一个单个的状态。智能体需要学习的是随机的奖励函数stochastic reward function。也就是说智能体在采样过程中，依据采样数据学习奖励函数分布，从而进一步指导接下来的动作(如果知道某个arm能够获得更多的奖励，那之后就一直选择这个arm，就能获得更多的奖励)。

对于多臂老虎机，描述起来都是比较简单的一个问题，但是最优解求解比较困难，对于上述问题看起来就没有什么思路。

Greedy strategy：

多想一下可能会有一个贪婪策略(greedy strategy)，就是选择当前平均奖励最高的那个arm，但是这种贪婪策略就没有考虑探索，比如有两个arm，当选择了其中一个arm-1这次得到奖励1，而另一个arm-2奖励为0，之后依据贪婪策略就一直选择arm-1，但arm-1实际的奖励为1的概率为0.1比arm-2奖励为1的概率0.9低呢？只不过刚好第一次被选中了而已，就很容易丢失掉探索，导致得到一个次优解。

$\varepsilon$ -greedy：

而 $\varepsilon$ -greedy方式说的是以一个 $\varepsilon$ 概率随机选择arm，而 $1-\varepsilon$ 概率选择greedy策略，也就是选择当前平均奖励最高的那个arm。由此可以看出收敛率(多快找到最优的arm)会取决于 $\varepsilon$ 。一旦找到最优的arm，

我们要衡量算法的好坏的话，需要定义一个指标，遗憾值(Regret)。

定义为某个arm的实际平均奖励值(或者称之为期望奖励)。如果我们知道了每个arm的平均奖励值，那我们可以找到具有最高平均奖励的那个arm，即：

$r^{*}=\max_{a}R(a) \\$

也就找到了具有最高平均奖励所对应的动作：

$a^{*} = arg\max_{a}R(a) \\$

但是我们并不知道每个arm的实际真实平均奖励，但是我们可以定义一个loss，用于衡量采取某个动作的好坏。对于每个动作与最优的动作比较，其二者之差可以定义为loss：

$loss(a)=r^{*}-R(a) \\$

time step下的期望累计遗憾可表示为：

$Loss_{n}=\sum_{t=1}^{n}loss(a_{t}) \\$

我们之前在讨论strategy的时候说过 $\varepsilon$ -greedy策略，那在定义好了衡量指标遗憾值regret时如何来进行理论分析呢？分析其本质规律。

如果 $\varepsilon$ 是个常量，time step足够大的话， $Pr(a_{t} \neq a^{*}) \approx \varepsilon$ (近似随机选择的arm都会后悔regret)，此时的期望累计遗憾值 $Loss \approx \sum_{t=1}^{n} \varepsilon =O(n)$ (这里只需要其是线性的就可以)。
如果 $\varepsilon_{t} \propto 1/t$ ，也就是随着time step增加， $\varepsilon$ 逐渐收敛。time step足够大的话， $Pr(a_{t} \neq a^{*}) \approx \varepsilon_{t}=O(\frac{1}{t})$ ，也就是说随着time step的增加，次优解会逐渐减少，此时的期望累计遗憾值 $Loss \approx \sum_{t=1}^{n} \frac{1}{t} =O(log n)$ (这里只需要其是对数级的就可以)。

线性级的遗憾值无法收敛，是无法得到最优解的，只能得到一个次优解。因此我们期望说能够找到一个遗憾值能尽快收敛的策略，若 $\varepsilon_{t} \propto 1/t$ 是可以使得遗憾值达到收敛的。

那经验平均奖励 $\tilde{R}(a)$ 与真实的平均奖励差多少呢？如果其两者差值存在一个上界(upper bound)，如 $|R(a)-\tilde{R}(a)| \leq \text{bound}$ ，随着数据的采集，上界逐渐收敛： $\lim _{n \rightarrow \infty} U B_{n}(a)=R(a)$ ，那经验平均奖励也将逼近真实的奖励。此时的最优算法求解就是在每一步选择最大的upper bound对应的那个arm，即 $\operatorname{argmax}_{a} U B_{n}(a)$ 。因此当upper bound收敛的时候，由于一直选取最大的upper bound对应的那个arm，我们得到的最优动作就是 $a^{*}$ 。

此时的问题就在于我们通过sample的方法是无法得到确定的upper bound的。就是基于采样的方法并不能得到真实的每个arm对应的奖励分布。我们可以采用概率的方法来表示，就是在采样过程中，小于等于上界是以一定的概率出现的，如： $\operatorname{Pr}(R(a) \leq f(a)) \geq 1-\delta$ ，依据霍夫丁不等式(Hoeffding’s inequality)有：

$\operatorname{Pr}(R(a) \leq \tilde{R}(a)+\sqrt{\frac{\log \left(\frac{1}{\delta}\right)}{2 n_{a}}}) \geq 1-\delta \\$

其中 $n_{a}$ 是arm a尝试的次数。 $\delta_{n}$ 通常设置为 $1/n^{4}$ ，使得算法收敛快一些。基于霍夫丁上界我们可以得到选择动作的最优策略：和记平台

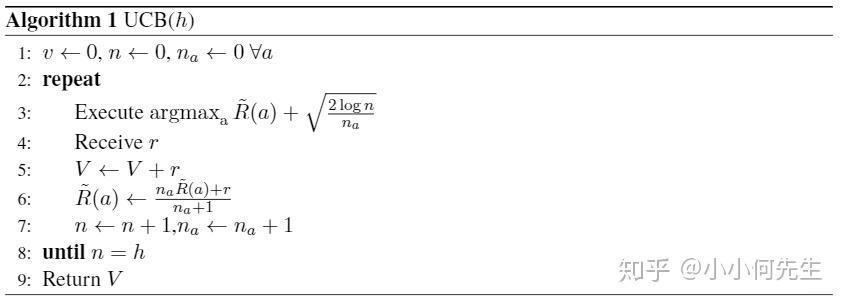
尽管上述算法理论上有收敛性保证，但是需要sample多次。

Bayesian Bandits能够更好地描述不确定性，在智能体平衡探索和利用的时候也是在决策不确定性，当智能体选择探索的时候不确定性更大一点，当选智能体择利用以往经验知识的时候不确定性就更小一点。用贝叶斯的方法来描述这种不确定性分布就是bayesian bandits。另一种能够获取更多状态信息的bandits方法称之为Contextual Bandits。

在开始贝叶斯多臂老虎机之前我们需要先定义贝叶斯学习(Bayesian Learning)。

当我们采取某个动作时，我们能够得到一个随机的奖励值 $r^{a}$ ，它是从某个分布中采样得到的。也就是说奖励的分布是不确定的，服从某个参数分布 $\theta$ ， $Pr(r^{a};\theta)$ 。而我们关心的是这个随机奖励 $Pr(r^{a};\theta)$ 的期望值 $R(a)=E[r^{a}]$ 。

因此我们可以把这种不确定性表述为一个先验分布 $Pr(\theta)$ ，我们需要做的事情就是通过采样获取数据 $r_{1}^{a},r_{2}^{a},\cdots,r_{n}^{a}$ ，依据这些采样得到的结果去估算后验分布 $Pr(\theta|r_{1}^{a},r_{2}^{a},\cdots,r_{n}^{a})$ 。一旦知道这个后验分布，也就是求解出了bandits的奖励分布。那这个后验分布怎么求呢？依据贝叶斯定理有：

$\operatorname{Pr}\left(\theta | r_{1}^{a}, r_{2}^{a}, \ldots, r_{n}^{a}\right) \propto \operatorname{Pr}(\theta) \operatorname{Pr}\left(r_{1}^{a}, r_{2}^{a}, \ldots, r_{n}^{a} | \theta\right) \\$

假设我们已经求得这个后验分布，我们就可以去估计下一个时刻的奖励 $r^{a}$ 的分布：

$\operatorname{Pr}\left(r^{a} | r_{1}^{a}, r_{2}^{a}, \ldots, r_{n}^{a}\right)=\int_{\theta} \operatorname{Pr}\left(r^{a} ; \theta\right) \operatorname{Pr}\left(\theta | r_{1}^{a}, r_{2}^{a}, \ldots, r_{n}^{a}\right) d \theta \\$

而我们关心的是每个arm的平均奖励，因此我们需要依据采样所得到的数据去估计平均奖励，如果 $\theta$ 是期望奖励 $\theta=R(a)$ ，有：

$\operatorname{Pr}\left(R(a) | r_{1}^{a}, r_{2}^{a}, \ldots, r_{n}^{a}\right)=\operatorname{Pr}\left(\theta | r_{1}^{a}, r_{2}^{a}, \ldots, r_{n}^{a}\right) \\$

到此，我们就可以计算最优策略。与之前的UCB算法对比：

UCB解决arm奖励分布不确定性用的是bound的方式，通过迭代求解bound来获得真实的期望奖励： $\operatorname{Pr}\left(R(a) \leq \text { bound }\left(r_{1}^{a}, r_{2}^{a}, \dots, r_{n}^{a}\right)\right) \geq 1-\delta$ 。
Bayesian techniques：并不通过求解upper bound，而是直接对其进行建模求解，直接求解arm奖励分布的概率。
Coin Example：

举个例子，假设我们有两枚硬币 $C_{1}$ 和 $C_{2}$ 。两枚硬币head朝上的概率不一样，可表示为：

$\begin{array}{l} R\left(C_{1}\right)=\operatorname{Pr}\left(C_{1}=\text { head }\right) \\ R\left(C_{2}\right)=\operatorname{Pr}\left(C_{2}=\text { head }\right) \end{array}\\$

期望在次掷币过程中最大化head的次数。那每次掷币我们因该选择哪个coin呢？可以量化每个coin的奖励分布 $r^{C_{1}},r^{C_{2}}$ 会满足一个伯努利分布 $\{0,1\}$ 。我们可以用一个参数 $\theta$ 表示获得奖励的分布：

$Pr(r^{C_{1}};\theta_{1})=\theta_{1}=R(C_{1})$
$Pr(r^{C_{2}};\theta_{2})=\theta_{2}=R(C_{2})$

若我们知道 $\theta$ 的真实值，我们可以依据 $\theta$ 来选择能够获得平均奖励最大的coin。设定 $\theta$ 的先验分布 $Pr(\theta)$ 是beta分布，则有：

$\operatorname{Beta}(\theta ; \alpha, \beta) \propto \theta^{\alpha-1}(1-\theta)^{\beta-1} \\$

其中 $\alpha -1$ 为掷到head的次数， $\beta -1$ 为尝试(tails)的次数，能拿到的奖励的期望值为 $E(\theta)=\frac{\alpha}{\alpha + \beta}$ 。

获得了 $\theta$ 的先验分布 $\operatorname{Pr}(\theta)=\operatorname{Beta}(\theta ; \alpha, \beta) \propto \theta^{\alpha-1}(1-\theta)^{\beta-1}$ 之后我们就可以计算其后验分布：

$\begin{aligned} \operatorname{Pr}(\theta | \text {head}) & \propto \operatorname{Pr}(\theta) \quad \operatorname{Pr}(\text {head} | \theta) \\ & \propto \theta^{\alpha-1}(1-\theta)^{\beta-1} \quad \theta \\ &=\theta^{(\alpha+1)-1}(1-\theta)^{\beta-1} \\ & \propto \operatorname{Beta}(\theta ; \alpha+1, \beta) \end{aligned}\\$

和

$\begin{aligned} \operatorname{Pr}(\theta | \text {tail}) & \propto \operatorname{Pr}(\theta) \quad \operatorname{Pr}(\text {tail} | \theta) \\ & \propto \theta^{\alpha-1}(1-\theta)^{\beta-1}(1-\theta) \\ &=\theta^{\alpha-1}(1-\theta)^{(\beta+1)-1} \\ & \propto \operatorname{Beta}(\theta ; \alpha, \beta+1) \end{aligned}\\$

当我们能够获得后验分布时，通过采样可以获得每个动作的后验平均奖励：

$R_{1}(a), \ldots R_{k}(a) \sim \operatorname{Pr}\left(R(a) | r_{1}^{a}, \ldots, r_{n}^{a}\right) \\$

然后估计经验平均奖励：

$\hat{R}(a)=\frac{1}{k} \sum_{i=1}^{k} R_{i}(a) \\$

选择动作的时候抽取能获得最大的奖励所对应的那个action $a=argmax_{a}\hat{R}(a)$ 就可以：

与Greedy Strategy对比，两者的不同就在于经验平均奖励一个是来自后验分布概率计算出来的 $\hat{R}(a)=\frac{1}{k} \sum_{i=1}^{k} R_{i}(a)$ ，一个是基于实际观测所得到的 $\tilde{R}=\frac{1}{n}\sum_{i=1}^{m}r_{i}^{a}$ 。因此Thompson Sampling基于后验概率算出来的奖励是具有不确定性的，因此探索程度会比贪婪策略更好，而随着观察数据的增多，模型越来越准确，这种探索也会随之减少。

在很多场合Context会提供更多的额外信息，比如像个性化推荐系统，Context会包含用户的年龄，性别，居住地等信息，而这些信息对个性化推荐系统都能起到辅助的作用。

contextual bandits用数学的方式描述为：

：状态集合，由一个特征向量描述 $x^{S}=\left(x_{1}^{S}, x_{2}^{S}, \ldots, x_{k}^{S}\right)$
lionking老虎机：动作集合，由一个与每个动作相关的特征向量描述 $x^{a}=\left(x_{1}^{a}, x_{2}^{a}, \ldots, x_{l}^{a}\right)$ 。
奖励空间 $\mathbb{R}$ 。

同样的是没有状态转移函数的。而我们要做的是找到一个策略 $\pi : x^{S}\rightarrow a$ ，它能够最大化期望奖励 $E(r | s, a)=E\left(r | \boldsymbol{x}^{s}, \boldsymbol{x}^{a}\right)$ 。为了能够获得奖励函数的模型，可以采用函数近似的方法，比如线性近似 $\tilde{R}_{w}(x)=w^{T} x$ 和非线性近似 $\tilde{R}_{\boldsymbol{w}}(\boldsymbol{x})=neuralNet (\boldsymbol{x} ; \boldsymbol{w})$ ，其中 $x=(x^{S},x^{a})$ 。

在线性近似的情况下采用贝叶斯的方法对其进行求解。假设参数 $\boldsymbol{w}$ 的先验分布为高斯分布，即：

$p d f(\boldsymbol{w})=N\left(\boldsymbol{w} | 0, \lambda^{2} I\right) \propto \exp \left(-\frac{\boldsymbol{w}^{T} w}{2 \lambda^{2}}\right) \\$

一旦我们知道了参数 $\boldsymbol{w}$ ，我们可以计算奖励的概率分布：

$p d f(r | \boldsymbol{x}, \boldsymbol{w})=N\left(r | \boldsymbol{w}^{T} \boldsymbol{x}, \sigma^{2}\right) \propto \exp \left(-\frac{\left(r-\boldsymbol{w}^{T} \boldsymbol{x}\right)^{2}}{2 \sigma^{2}}\right) \\$

基于贝叶斯定理可以计算后验概率求得参数 $\boldsymbol{w}$

$\begin{array}{l} p d f(\boldsymbol{w} | r, x) \propto p d f(\boldsymbol{w}) \operatorname{Pr}(r | x, \boldsymbol{w}) \\ \propto \exp \left(-\frac{\boldsymbol{w}^{T} \boldsymbol{w}}{2 \lambda^{2}}\right) \exp \left(-\frac{\left(r-\boldsymbol{w}^{T} x\right)^{2}}{2 \sigma^{2}}\right) \\ =N(\boldsymbol{w} | \mu, \Sigma) \end{array}\\$

其中 $\mu=\sigma^{-2}\sum xr$ ， $\Sigma=\left(\sigma^{-2} x x^{T}+\lambda^{-2} I\right)^{-1}$ 。到此整个的求解框架就差不多完事了。假设我们有一个状态动作对 $(x^{S},x^{a})=x$ ，我们期望去预测它的奖励，可以采用预测后验概率分布的方式得到：

lionking老虎机 lionking老虎机lionking老虎机 $\begin{aligned} p d f(r | \boldsymbol{x}) &=\int_{\boldsymbol{w}} N\left(r | \boldsymbol{w}^{T} \boldsymbol{x}, \sigma^{2}\right) N(\boldsymbol{w} | \boldsymbol{\mu}, \Sigma) d w \\ &=N\left(r | \sigma^{2} \boldsymbol{x}^{T} \boldsymbol{\mu}, \boldsymbol{x}^{T} \boldsymbol{\Sigma} \boldsymbol{x}\right) \end{aligned}\\$

lionking老虎机：求通俗解释下bandit老虎机到底是个什么东西？

一	二	三	四	五	六	日
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30

lionking老虎机：求通俗解释下bandit老虎机到底是个什么东西？

相关文章 :